Spaced Repetition
Spaced repetition is a learning technique that incorporates increasing intervals of time between subsequent review of previously learned material in order to exploit the psychological spacing effect, the phenomenon whereby animals (including humans) more easily remember or learn items when they are studied a few times spaced over a long time span ("spaced presentation") rather than repeatedly studied in a short span of time ("massed presentation").
Following Lietner System, we are going to use a fixed number of learning boxes - in our specific case we will use four boxes. All cards will initially be placed in the first box. When a card is presented to the student for recognition, there are two possible outcomes:
- if the card is correctly recognized, it will be moved to the next box
- if the user fails to recognize the card, the card will be moved into the first box
Extending this method to improve long-term memory, once a card reaches the last box and it is correctly recognized, it will also be moved back into the first box for another round of learning (achieving therefore level two of learning). All cards must go through three levels of learning. At any point in time, a failure will bring back the failed card to the first box, resetting it to level one as well.
This method can be summarized in the following two graphs. Each box has 3 levels of learning (L1, L2 and L3). All cards start from Box 1 / Level 1 and start moving following the next relationships shown in the first graph. .
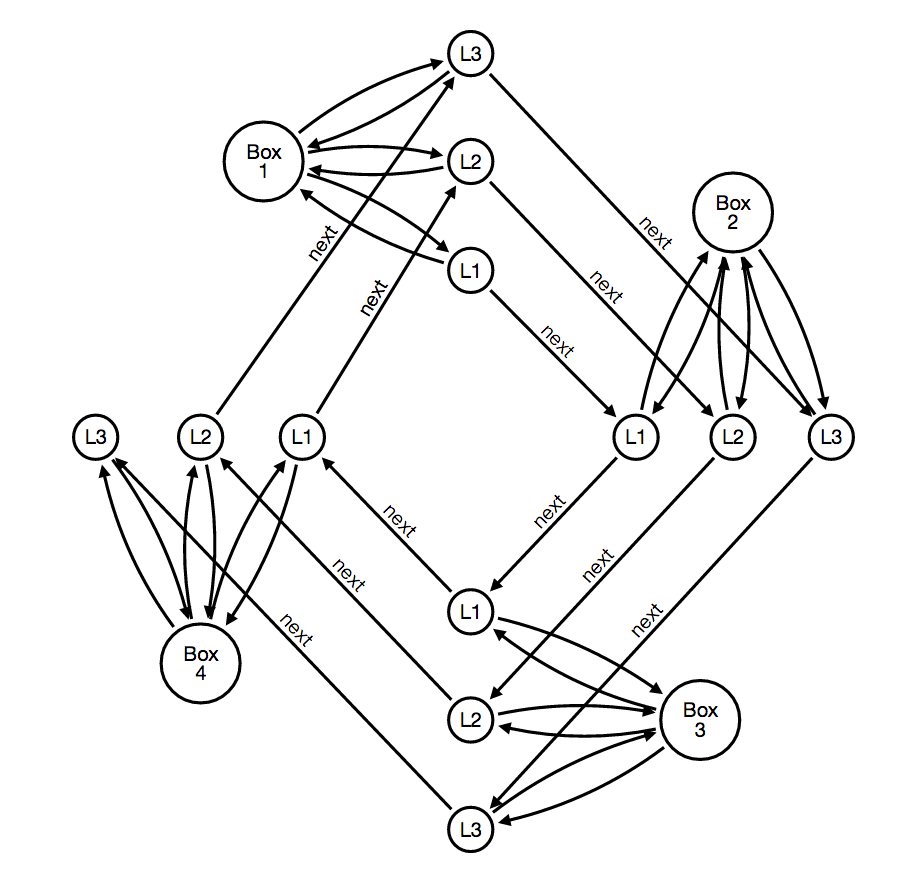
A failure moves the card along the back relationship shown in the second graph.
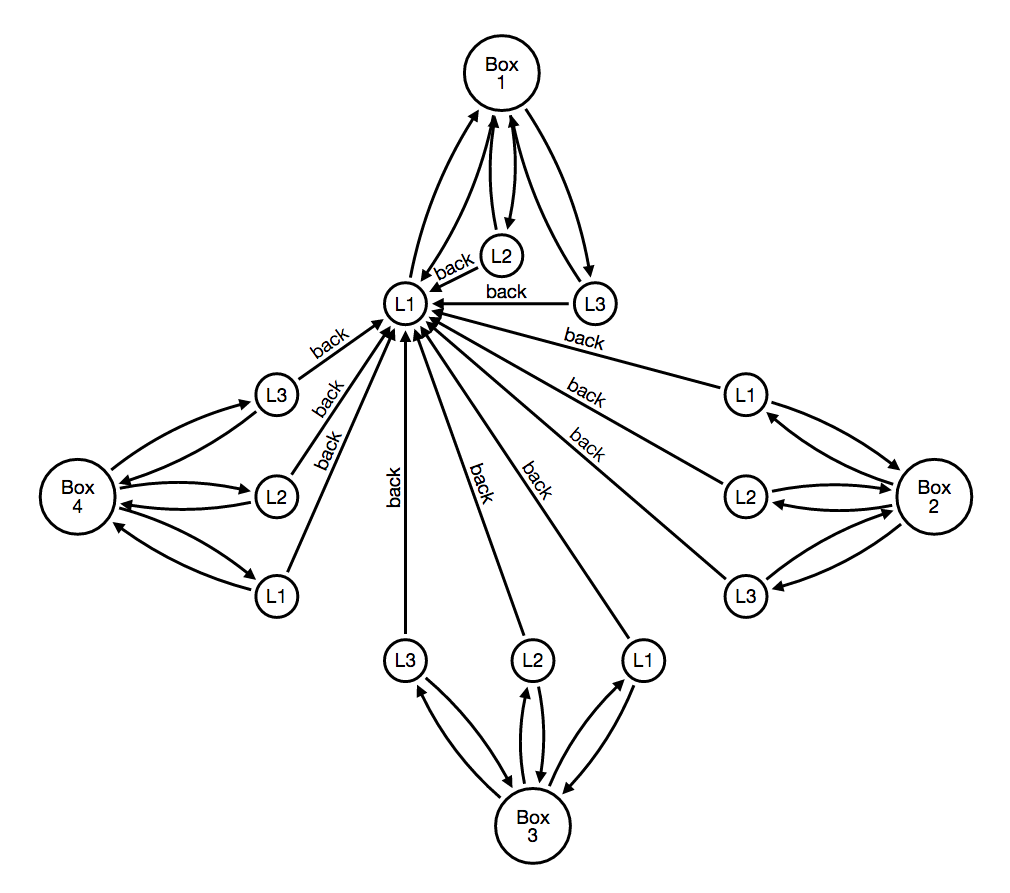
These graphs essentially embed most of the business logic into nodes and relationships.
The Unit of Study
Next, let's take a look at the relationships between the student, the *cards** that he is learning, and the boxes. Because we want to minimize repetition of data, each card will be a single node in the graph database and will be share across all students. Furthermore, there will be one single set of boxes (and levels), shared by all students as well.
This means that we need to find a way to represent which cards are in which box at which learning level for which student. To hold this piece of information, we introduce the concept of unit of work which connects a student with the cards that he is currently learning, while keeping track of the level of learning achieved so far.
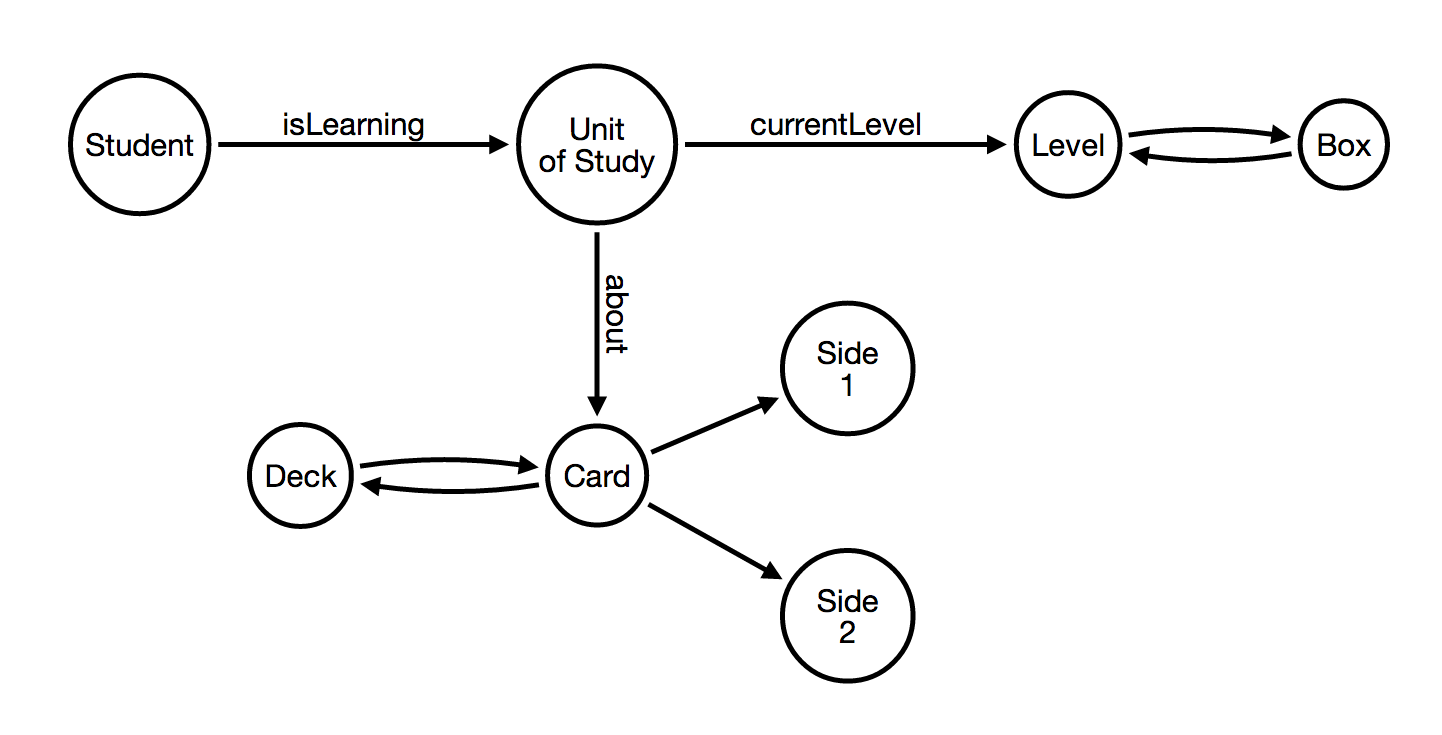
The Card
The bottom part of this graph introduces the card. Let's add a bit more detail to this representation, taking a look at what is actually stored on each side of the card.
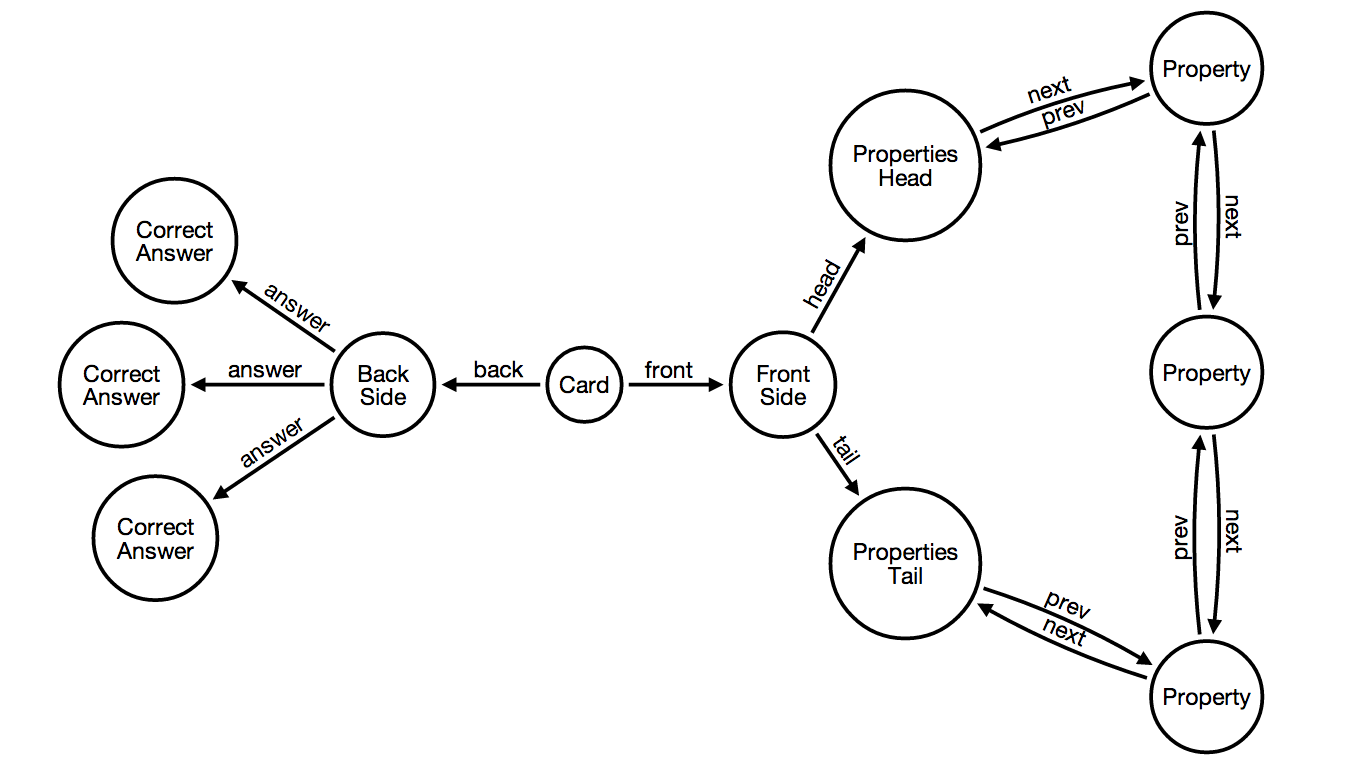
Each card must have an ID, a Name and a Category (used also to represent different categories of cards in different ways). Furthermore, each card must have a front side and a back side.
The front side is used when studying new units of study, and therefore it contains a list of properties. Different type of cards will contain different sets of properties, obviously. In this implementation, each property must contain the following fields:
- title: the title of the property -- for example, a set of cards to study Japanese kanji could use Radicals, Readings, Meaning, etc.
- class: this is the CSS class that will be assigned to the DIV wrapping the property
- body: this is the actual HTML body of the property - it should be as simple as possible with no extra styling applied (all CSS styling should be derivable from the property class above) and it should only contain:
- header tags
- paragraph tags
- images
The back side is used to verify the knowledge of the card, and therefore it contains no text of its own, just one or more acceptable answers. This implementation will always require the user typing out an answer because typing out the answers actually reinforces knowledge better than choosing an answer out of a random set (multiple choice answers).
Cards Relationships
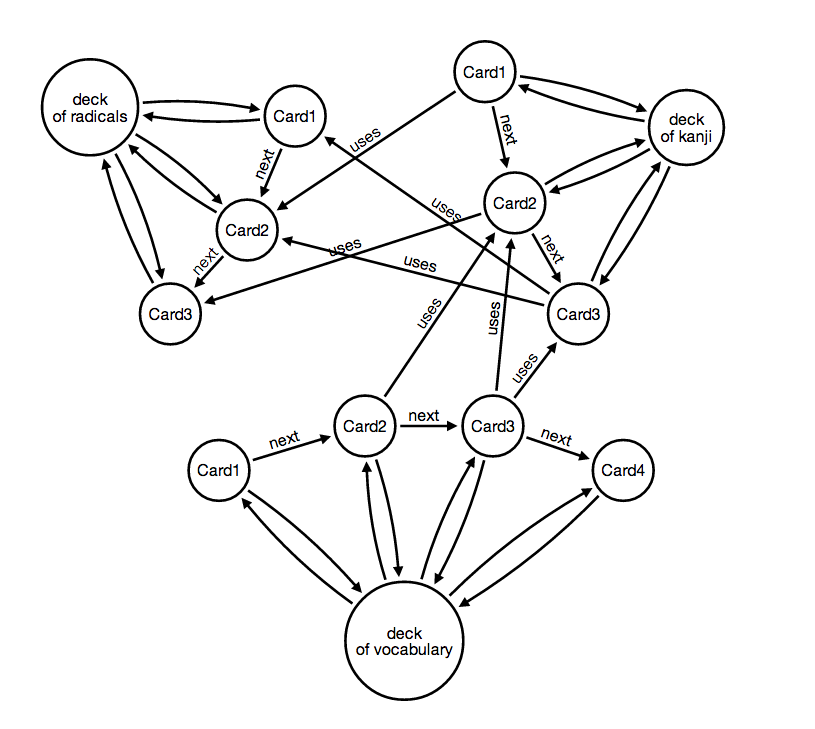
Now that we have seen how cards are built inside, let's take a quick look at how cards are related. 1. All cards have a two-way relationship with the deck they belong to. I am not sure if this is necessary at all from a Neo4J perspective, maybe a single first relationship from the deck to the first card might be sufficient, or maybe decks don't even need to exist and could be substituted by labels in each card. 2. All cards in a deck are linked together by next relationships, which enforce the order in which they should be learned. 3. Some cards might have extra uses relationships either within the same deck or with cards of different decks.
For example, in the following figure, we have three decks to learn Japanese. The first deck has all the radicals, the second deck contains all kanji characters, and the third deck contains all vocabulary. Since kanji characters are made of radicals and vocabulary words are made of kanji characters, one can see how tightly connected these three sets are.
Summing Up
Let's try to put the gist of the problem together in a single graph. To make things easier, let's consider a simple scenario:
- we have one deck with 9 cards (C1, C2,...)
- the learning boxes have only one level (L1)
- a student has already added 4 cards to his learning set; card C1 has already been successfully tested, therefore is now in Box2; the other 3 cards (C2, C3 and C4), are still in Box1, ready to be tested.
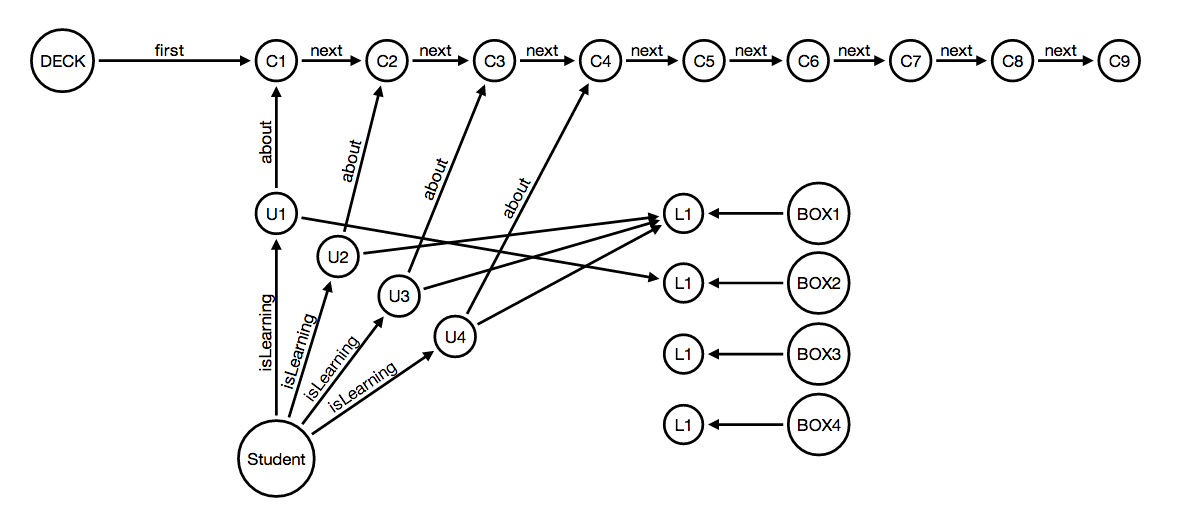
The graph above shows the 4 units of study, U1 through U4, connected to the respective cards, C1 through C4, and connected to the current knowledge level achieved by the student for each of the cards (U1 is in L1 of Box2, while all other units of study are still in L1 of Box1).
Let's write some pseudocode to process the next review phase.
var levels = {L1, L2, L3};
var boxes = {B1, B2, B3, B4};
// let's first review all units in L1/B1, then L1/B2, L1/B3, L1/B4, etc.
foreach(level in levels) {
foreach(box in boxes) {
var units = GetUnitsOfStudy(user, level, box);
foreach(unit in units) {
if((time.now()-unit.lastUpdated) > box.timeToReview) {
var answer = unit.Review();
if(answer in unit.card.back.answers) {
unit.currentLevel = unit.currentLevel.next;
}
else {
unit.currentLevel = unit.currentLevel.back;
}
unit.lastUpdated = time.now();
}
}
}
}
Do you want to help me write the Cypher query that gets the next card to be added to L1/B1? The answer is C5, obviously, because:
- card C5 has no incoming [about] relation connected to any unit of study connected by an [isLearning] relation to the student
- the card previous to C5 has an incoming [about] relation connected to an unit of study (U4) connected by an [isLearning] relationship to the student.
Leave your answer in the comments below!
For your convenience, I have created a Neo4J Graph Gist that you can use to play with the sample dataset described above, running cypher queries against it.
Finding the Next Card to be Studied
Here is my attempt to solve the Gist above. If you know of a better way to achieve the same result, please let me know!
OPTIONAL MATCH
(S:Student)-[:ISLEARNING]->(U:UnitOfStudy)-[:ABOUT]->(lastCard:Card)-[:NEXT]->(nextCard:Card)<-[:HASCARD]-(D1:Deck)
WHERE
NOT ()-[:ABOUT]->(nextCard)
AND S.name = "Student2"
AND D1.name = "Deck"
OPTIONAL MATCH (D2:Deck)-[:FIRST]->(firstCard:Card)
WHERE D2.name = "Deck"
RETURN COALESCE(nextCard, firstCard)
This query has two OPTIONAL MATCH clauses. This is to take in account the special case in which no cards have been studied yet by the student. In this case, the first OPTIONAL MATCH will return null and therefore the COALESCE function (which returns the first non null argument) will return firstCard instead.
